Understanding Gaussian Process Machine Learning Fundamentals

Gaussian process (GP) machine learning offers a powerful, probabilistic approach to regression and classification. Unlike traditional methods that give single-point predictions, GPs provide a full probability distribution. This means you receive a prediction and a measure of its uncertainty, similar to a confidence interval. This is invaluable when understanding the confidence level is as important as the prediction itself.

Key Components of a Gaussian Process

Two functions define a Gaussian process: the mean function and the covariance function (also called the kernel). The mean function represents the average prediction across all possible functions the GP can model. The covariance function describes the relationship between predictions at different input points.

For instance, the squared exponential kernel is a common covariance function. It assumes that input points close together will have similar predictions. This ability to link predictions allows GPs to capture complex data relationships. Want to brush up on your data science basics? Check out this resource: How to master data science fundamentals.

The Power of Uncertainty Quantification

The ability to quantify uncertainty is a hallmark of Gaussian processes. This comes from their inherent probabilistic nature. GPs don’t just learn one function to fit the data; they learn a distribution over functions. This distribution reflects the model’s uncertainty about the true underlying function, a valuable feature when dealing with limited or noisy data. By providing uncertainty measures, GPs help decision-makers assess risks associated with predictions.

Gaussian processes have a rich mathematical background originating from the work of Carl Friedrich Gauss and the Gaussian (normal) distribution. In machine learning, GPs provide a non-parametric Bayesian approach. Unlike parametric models that assume a fixed functional form, GPs define a distribution over possible functions that fit the data, enabling robust uncertainty quantification. Learn more here: Learn more about Gaussian processes.

Advantages of Gaussian Processes in Machine Learning

• Flexibility: GPs can model a wide variety of functions thanks to the flexible choice of covariance function.
• Interpretability: The covariance function offers insights into the relationships between inputs and predictions.
• Robustness to Overfitting: Due to their Bayesian nature, GPs are less prone to overfitting, particularly with smaller datasets.

These advantages make Gaussian process machine learning a powerful tool for complex problems where quantifying uncertainty is crucial.

From Theory To Practice: The GP Evolution Story

Gaussian process machine learning (GPML) has come a long way. What started as a theoretical idea has blossomed into a practical tool used in real-world situations. Its journey, marked by important discoveries and increased computing power, shows just how vital uncertainty quantification is in machine learning.

The Rise of Data-Driven Learning and GPs

Machine learning models used to be primarily knowledge-driven, based on rules set by experts. However, the 1990s saw a change towards data-driven methods. Gaussian processes in machine learning emerged during this time, aligning with the growing trend of using data to create models. This change highlighted the need for models that could not only make predictions but also show how confident they were in those predictions. Discover more insights about the timeline of machine learning. This surge in popularity cemented GPs as a key component of modern machine learning.

Kernel Methods and the GP Advantage

Gaussian processes and kernel methods both aim to identify patterns in data. However, GPs have a significant advantage: they provide reliable uncertainty estimates. Kernel methods primarily map data to a higher-dimensional space to make analysis simpler. GPs, on the other hand, create a probability distribution of possible functions that could fit the data. This probabilistic approach allows GPs to determine the uncertainty associated with their predictions. This is especially useful when knowing the confidence level is critical.

Breakthroughs Enabling Large-Scale Applications

In the beginning, the complex calculations involved in GPs limited their use to smaller datasets. Over time, improvements in computational methods and the development of more effective algorithms enabled larger-scale GP applications. Important publications, such as the 2004 book “Gaussian Processes for Machine Learning” by Rasmussen and Williams, organized the existing research. This provided a unified framework for researchers and practitioners, helping to boost adoption and encourage further research.

Industry Adoption and Early Adopters

Different industries adopted GPs at different paces. Some sectors, such as geostatistics and robotics, were early adopters. These fields needed ways to model spatial uncertainty and navigate unpredictable environments. Other fields, including healthcare and finance, have gradually started using GPs in their work. They recognized the importance of understanding uncertainty for tasks like diagnosis and risk assessment. Continued progress in developing scalable GP methods promises even wider adoption in the future.

Performance Reality Check: What The Numbers Actually Show

Gaussian Process (GP) machine learning models offer unique advantages, especially their ability to quantify uncertainty. However, understanding their performance characteristics is vital for making informed decisions about their practical use. This means examining the computational realities of GPs, acknowledging both their strengths and weaknesses.

Computational Complexity and Practical Implications

One of the primary challenges with GPs is their computational complexity, which scales as O(n³) with the number of training points (n). This can make them computationally expensive for large datasets. For instance, working with datasets larger than 10,000 points often necessitates specialized approximation techniques. However, this computational cost comes with a major advantage: highly accurate uncertainty estimates. This is essential for applications where knowing the confidence level of a prediction is paramount.

Additionally, Gaussian process models shine at modeling complex, nonlinear relationships with built-in uncertainty quantification. Quantitative benchmarks show that for regression tasks with moderate sample sizes, GPs frequently outperform neural networks in prediction accuracy, all while providing calibrated confidence intervals. Learn more about Gaussian process machine learning performance here.

Benchmarking Performance: Accuracy vs. Efficiency

The infographic below illustrates the interplay between sample size, mean squared error, and predictive variance in a typical GP regression task. It plots Mean Squared Error and Predictive Variance against increasing Sample Sizes.

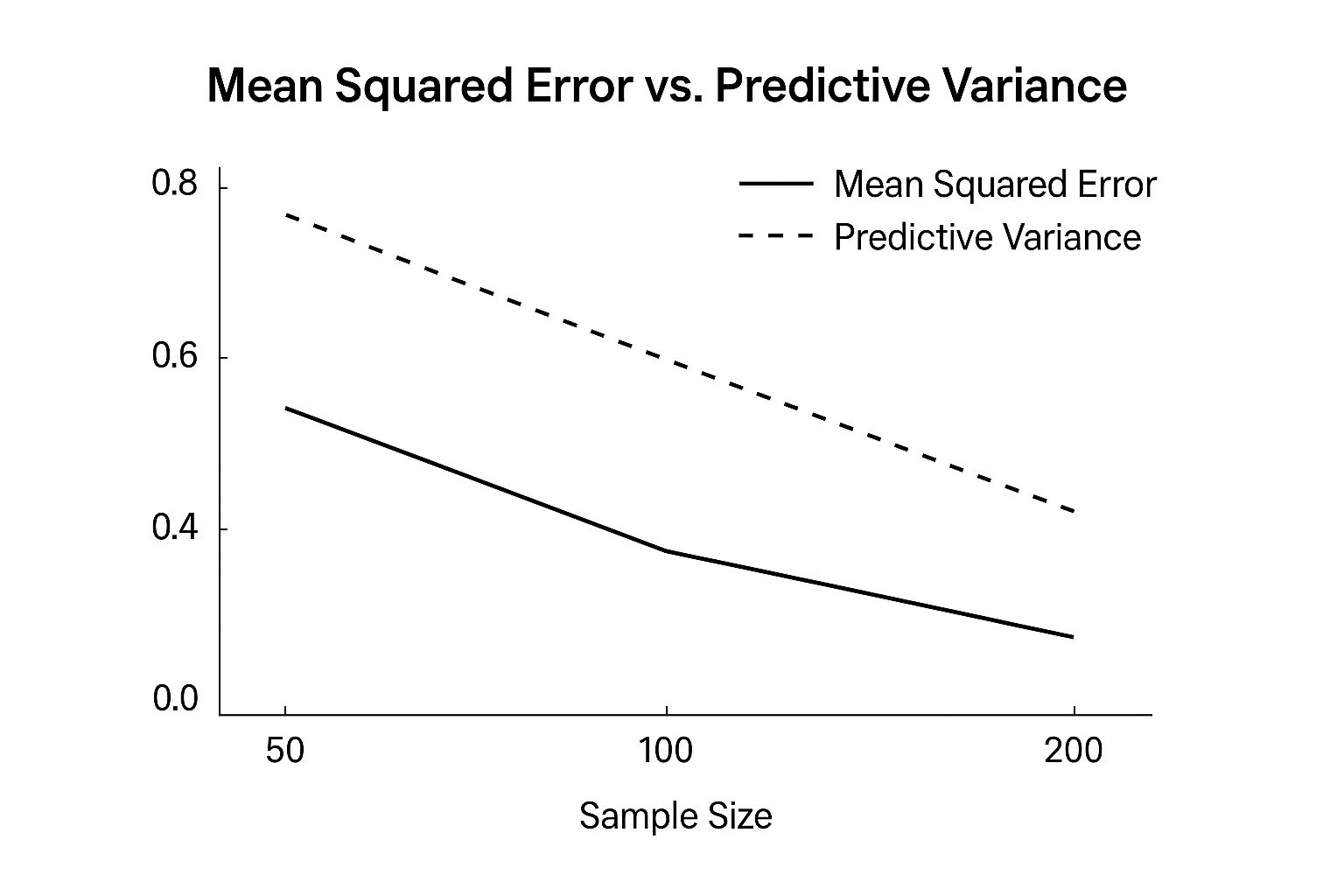
As the sample size grows, the mean squared error decreases, indicating improved accuracy. At the same time, the predictive variance also decreases, reflecting increased confidence in the predictions. This underscores the inherent trade-off between accuracy, dataset size, and the computational burden linked to larger datasets in GP models.

To further illustrate these comparisons, let’s look at a table summarizing the performance differences between Gaussian Processes and other common machine learning methods.

To understand the performance trade-offs associated with different machine learning algorithms, the following table provides a comparative analysis across various metrics.

Method	Dataset Size Limit	Uncertainty Quantification	Accuracy (MSE)	Computational Complexity
Gaussian Process	Moderate (up to ~10,000 without approximations)	Excellent	High (for moderate datasets)	O(n³)
Linear Regression	Large	Limited	Moderate (for linear relationships)	O(n)
Support Vector Machines	Large	Limited	High	Varies (generally between O(n²) and O(n³))
Neural Networks	Very Large	Challenging	High (can be very high with large datasets)	Varies (depends on architecture)

As shown in the table, while Gaussian Processes excel in uncertainty quantification and achieve high accuracy on moderately sized datasets, their computational complexity limits their applicability to very large datasets without employing approximation techniques. Other methods like Support Vector Machines and Neural Networks can handle larger datasets but often lack the robust uncertainty quantification offered by GPs.

Pushing the Boundaries with Approximation Techniques

Despite the computational challenges, modern approximation methods are extending the use of Gaussian process machine learning to larger datasets. These techniques enable practitioners to harness the strengths of GPs even with substantial amounts of data. This creates opportunities for applications in areas like image recognition and natural language processing, where large datasets are common. Understanding these methods empowers data scientists to apply Gaussian process methods effectively to real-world problems.

Real-World Success Stories That Actually Matter

Moving beyond the theoretical, let’s delve into the practical applications of Gaussian process (GP) machine learning. These real-world examples showcase the tangible benefits GPs bring to various industries.

Healthcare: Improving Diagnostic Accuracy

Accurate diagnoses are paramount in healthcare. Gaussian processes play a vital role in diagnostic systems where understanding the confidence level of a prediction can be crucial.

Some diagnostic imaging systems, for instance, leverage GPs to analyze medical images. The uncertainty quantification offered by GPs enables doctors to assess the reliability of the AI’s diagnosis. This is especially valuable when dealing with images that present ambiguous or complex features. This added layer of confidence empowers medical professionals to make more informed decisions, potentially leading to better patient outcomes.

Finance: Managing Risk with Confidence

Financial institutions depend on precise risk assessments. Gaussian process machine learning is well-suited for this task due to its ability to provide dependable uncertainty estimates. These estimates are frequently preferred, often aligning with regulatory requirements.

This inherent interpretability makes GPs particularly appropriate for applications such as credit scoring and fraud detection. In these areas, comprehending the rationale behind a decision is as important as the decision itself. Furthermore, the probabilistic nature of GPs enables financial analysts to model complex market dynamics and factor in various uncertainties into their evaluations.

Robotics: Navigating Uncertainty in the Real World

The unpredictable nature of real-world environments poses unique challenges for machine learning models in robotics. Gaussian processes prove invaluable in helping autonomous systems navigate these uncertainties safely. Self-driving cars, for example, utilize GPs to manage unexpected obstacles or changing road conditions.

The model’s capacity to quantify uncertainty allows the vehicle to make safer decisions in ambiguous situations by considering the probability of different outcomes. This capability enhances the overall robustness and dependability of autonomous navigation systems.

Beyond Specific Industries: Broader Applications of Gaussian Processes

The utility of Gaussian process machine learning extends beyond just a few sectors. From geostatistics in the mining industry to active learning systems that optimize expensive experiments, GPs offer adaptable solutions.

• Geostatistics: In mining, GPs model ore deposits and optimize exploration strategies. This empowers mining companies to make more efficient decisions about excavation locations, leading to significant savings in both time and resources.
• Active Learning: When acquiring data is costly or time-intensive, Gaussian processes can guide experimental design. By concentrating on collecting data from the most informative areas, GPs reduce the total number of experiments required. This has far-reaching implications for both scientific research and engineering projects.

These are just a glimpse into the potential of Gaussian process machine learning. As research progresses and computational resources advance, we anticipate even more groundbreaking applications of GPs. The capacity to quantify uncertainty, model complex relationships, and adapt to new data establishes GPs as a versatile tool for tackling real-world challenges across diverse fields. For more in-depth information on Gaussian processes, explore the resources available at DATA-NIZANT.

Implementation That Actually Works In Practice

Implementing Gaussian process machine learning (GPML) effectively goes beyond theoretical understanding. This section offers practical strategies employed by seasoned practitioners to construct successful GP models. This involves careful consideration of kernel selection, hyperparameter optimization, and selecting the correct implementation method.

Kernel Selection: The Heart of Your GP

The kernel, also known as the covariance function, is the cornerstone of a Gaussian process. It defines how the model captures the relationships between data points. Selecting the appropriate kernel is paramount for model performance. The squared exponential kernel is frequently used. This kernel operates under the assumption that points in close proximity share similar output values.

However, other kernels, such as the Matérn kernel, offer more flexibility in modeling diverse function types. The Matérn kernel, for instance, provides control over the smoothness of the function, making it adaptable to various datasets.

Hyperparameter Optimization: Finding the Sweet Spot

Gaussian processes utilize hyperparameters that govern the kernel’s behavior. These hyperparameters require meticulous tuning. Maximum likelihood estimation (MLE) is a widely-used technique that aims to identify the hyperparameter values maximizing the likelihood of the observed data.

Cross-validation is another approach that assesses model performance on different data subsets to determine the optimal hyperparameters. The ideal approach depends on the specific dataset and available computational resources.

Preprocessing: Setting the Stage for Success

Data preprocessing is critical for achieving optimal GP performance. This encompasses scaling input features and addressing missing values. Standardization, a process where features are transformed to have a zero mean and unit variance, can enhance model stability and accelerate convergence speed. Imputation techniques can effectively fill in missing data, ensuring the GP model can handle the entire dataset.

Exact vs. Approximate Methods: Choosing the Right Tool

Gaussian process inference presents a choice between exact and approximate methods. Exact methods, while precise, are computationally demanding, scaling at O(n³), which limits their application to smaller datasets. Approximate methods, like variational inference and inducing point methods, provide scalability by approximating the full GP. The choice depends on balancing computational costs and desired accuracy. You might find this resource helpful: How to master your machine learning infrastructure.

Libraries and Frameworks: Simplifying Implementation

Several libraries and frameworks streamline the implementation of Gaussian processes. In Python, GPy and GPflow are popular choices. These libraries offer pre-built kernels, optimization routines, and visualization tools. Understanding their strengths and limitations is vital for selecting the right tool for your needs, which often comes down to familiarity with specific libraries.

To help you choose the right framework, take a look at the comparison table below:

To assist in selecting the best framework for your Gaussian Process implementation, the following table summarizes key features of popular options:

Gaussian Process Implementation Framework Selection Guide
Comparison of popular GP libraries, their features, scalability limits, and best use cases

Library/Framework	Language	Max Dataset Size	Key Features	Best Use Case
GPy	Python	Medium (10k-100k)	User-friendly, versatile kernels	Prototyping, moderately sized datasets
GPflow	Python	Large (100k+)	TensorFlow integration, scalable inference	Large datasets, deep learning integration
GPyTorch	Python	Large (100k+)	PyTorch integration, scalable inference	Large datasets, deep learning integration
scikit-learn GaussianProcessRegressor	Python	Small (<10k)	Simple, easy to use	Small datasets, baseline comparisons

As shown in the table, the choice of framework depends heavily on the size of your dataset and the need for deep learning integration. For larger datasets, GPflow and GPyTorch are often preferred.

Common Pitfalls and Solutions: Navigating the Challenges

Implementing Gaussian processes can present challenges, even for experienced developers. Numerical instability is a common issue that arises when dealing with ill-conditioned covariance matrices. Techniques such as Cholesky decomposition with jitter can mitigate this problem. Another frequent pitfall is selecting an unsuitable kernel for the data. Careful analysis of data characteristics and exploration of different kernel options are crucial. Addressing these challenges leads to more robust and reliable GP models.

Cutting-Edge Developments Worth Watching

Gaussian Process (GP) machine learning is a constantly evolving field. This section explores some exciting innovations that are pushing the boundaries of what’s possible with GPs. These advancements tackle important challenges, like handling large datasets and working with complex data, unlocking new potential for GP use across diverse fields.

Deep Gaussian Processes: Combining the Best of Both Worlds

Deep Gaussian Processes (DGPs) represent a significant leap forward. They combine the strengths of traditional GPs with the power of deep learning architectures. DGPs stack layers of GPs, creating a hierarchy of functions. This structure allows them to capture intricate, non-linear relationships in data, something single-layer GPs struggle with. Imagine it as blending the careful uncertainty management of GPs with the flexibility of deep neural networks. This blend offers a powerful approach to tackling complex datasets.

Variational Inference: Making GPs Scalable

A major hurdle for traditional GPs is their computational cost, which increases dramatically with the dataset size. Variational inference offers a practical solution. These methods approximate the true distribution of the GP, allowing us to analyze much larger datasets than before. This breakthrough opens doors to using GPs in applications previously deemed computationally impossible.

Expanding the Scope: Multi-Output GPs and Transfer Learning

Many practical problems involve predicting multiple related outcomes. Multi-output Gaussian Processes (MOGPs) handle this by modeling the connections between different output variables. This is especially helpful in fields like sensor networks or financial modeling, where many related metrics are measured or predicted together. Furthermore, transfer learning is now being applied to GPs. This allows models trained on one dataset to be adapted to similar but distinct datasets, broadening the applicability of GP models.

Looking Ahead: Quantum Enhancements and Novel Approximations

The future of Gaussian process machine learning is bright, with research continually pushing the field forward. Scientists are investigating quantum-enhanced methods to accelerate GP calculations, potentially overcoming some inherent scaling limitations. New approximation techniques are also under development, aiming to make large-scale GP applications practical for even bigger datasets. These methods strive for a balance between computational efficiency and the reliable probabilistic nature of GPs, which is crucial for applications where uncertainty quantification is paramount. For a deeper dive into Gaussian processes and their uses, visit DATA-NIZANT for detailed analyses and helpful resources.

Your Practical Roadmap To GP Success

This guide simplifies the complexities of Gaussian Process Machine Learning (GPML) into a practical roadmap for successful implementation. We’ll explore decision frameworks, checklists, and exercises to guide you from project assessment to deployment.

Is GPML Right For Your Project?

The first step is determining if GPML is the right approach. Consider these key factors:

• Dataset Size: GPs shine with small to medium-sized datasets (up to approximately 10,000 data points without approximations). For larger datasets, explore alternative methods or approximation techniques for GPs.
• Need for Uncertainty Quantification: If grasping prediction confidence is vital for your application, GPs are an excellent choice due to their inherent probabilistic nature.
• Computational Resources: The O(n³) computational complexity of GPs can be resource-intensive. Ensure you have sufficient resources or consider approximations.

Essential Prerequisites and Learning Path

Before implementation, solidify your foundation in these areas:

• Probability and Statistics: A strong understanding of Gaussian distributions, covariance, and Bayesian principles is fundamental.
• Linear Algebra: Familiarity with matrix operations and linear systems is crucial for working with covariance matrices.
• Machine Learning Fundamentals: A firm grasp of supervised learning, model evaluation, and hyperparameter tuning is essential.

A recommended learning path involves progressing from basic kernel methods to understanding the probabilistic framework of Gaussian processes. Hands-on practice with GP libraries like GPy and GPflow is key to developing practical proficiency. You might be interested in How to master MLOps best practices.

Avoiding Common Beginner Mistakes

Many GP projects encounter setbacks due to these avoidable mistakes:

• Incorrect Kernel Selection: A kernel misaligned with the data’s characteristics can significantly hinder performance. Experiment with different kernels and understand their implications.
• Ignoring Hyperparameter Tuning: Optimal hyperparameters are essential for optimal performance. Overlooking this step results in subpar models.
• Insufficient Data Preprocessing: Neglecting to scale input features or address missing values can negatively impact model stability and convergence.

Building Practical Competence

To solidify your understanding, engage in practical exercises and projects:

• Regression Tasks: Implement GPs to predict continuous variables like stock prices or sensor data.
• Classification Problems: Discover how GPs apply to classification tasks such as image recognition or spam detection.
• Experiment with Different Kernels: Develop an intuitive understanding of how kernel selection influences a model’s ability to capture diverse data relationships.

By following this roadmap and emphasizing practical application, you can harness the power of Gaussian process machine learning.