The Power Behind K Fold Cross Validation

K fold cross validation has become a cornerstone of machine learning for evaluating model performance. It provides a more robust and reliable assessment than traditional single train-test splits. This method divides your dataset into k equal parts, called folds.

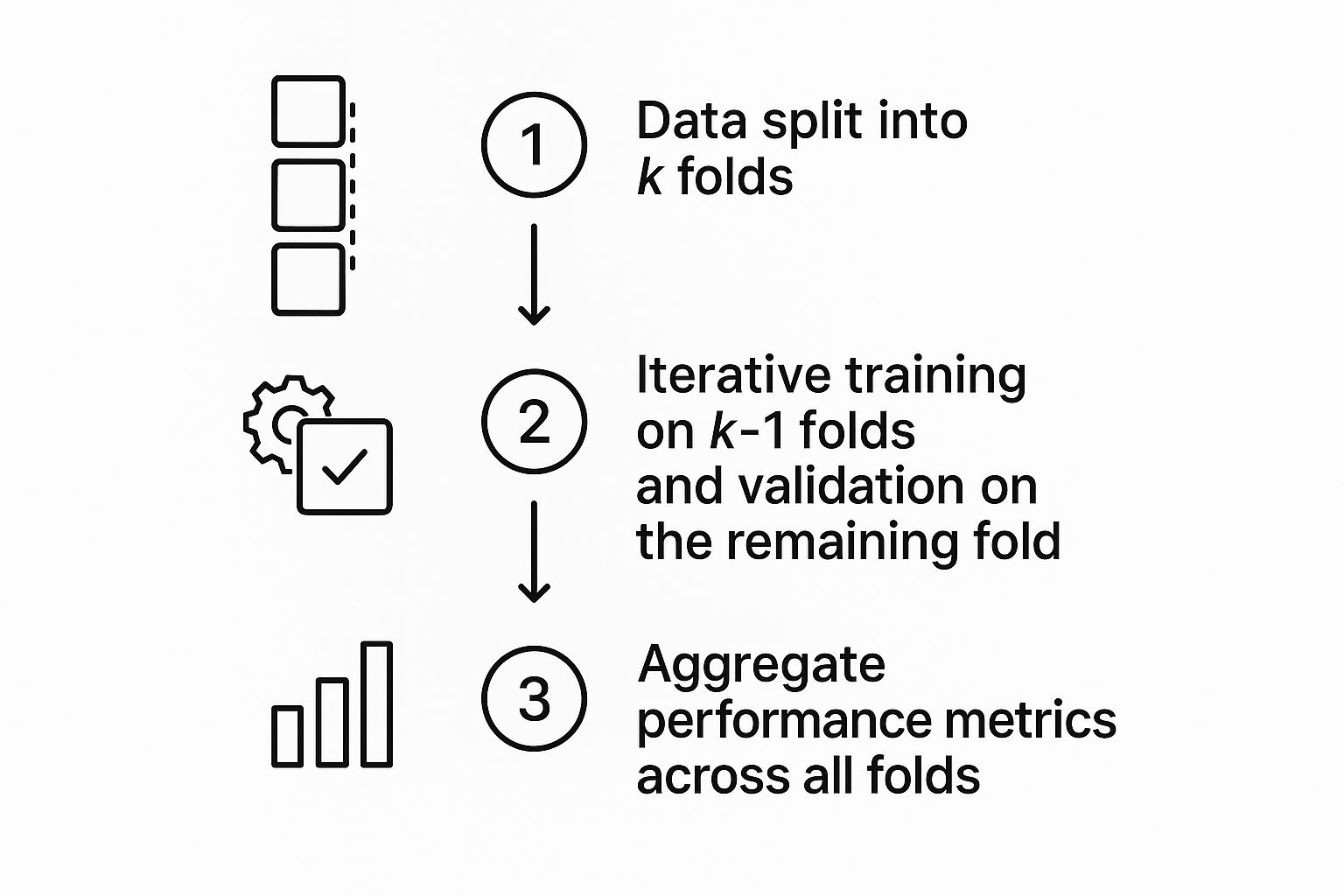
The diagram above illustrates the process. It shows the data splitting, the iterative training and validation process, and the final aggregation of performance metrics. This iterative approach ensures each data point contributes to both training and validation, providing a comprehensive view of model performance. This leads to a more stable and less biased estimate of how well the model generalizes to unseen data.

Why K Fold Cross Validation Matters

K fold cross validation’s core strength lies in mitigating the risks of overfitting. Overfitting occurs when a model performs very well on training data but poorly on new data. By rotating through the folds, the model is exposed to diverse data subsets, reducing its reliance on any single portion. This makes the evaluation more representative of real-world scenarios where the model encounters unfamiliar data.

K fold cross validation offers a more granular understanding of model performance across different data segments. This is particularly helpful for identifying potential weaknesses and biases.

One significant advantage of k-fold cross-validation is its ability to provide a robust performance estimate. The dataset is divided into k equal (or approximately equal) segments called folds. Each fold serves as a validation set once, with the remaining folds forming the training set. This is repeated k times.

This ensures each data point is used for both training and validation. For instance, a study comparing machine learning algorithms used k-fold cross-validation. It identified the most robust model with a 92% accuracy rate across all folds. Learn more about cross-validation from this resource on Cross-Validation (Statistics)). For advice on avoiding common issues, check out these Automated Testing Best Practices.

Choosing the Right K Value

Selecting the appropriate “k” value is crucial. A small k (like 2) can lead to high variance in performance estimations. A large k can be computationally intensive. A common choice is 10, balancing computational efficiency and reliable results. However, the ideal k depends on the specific dataset and available computational resources.

With limited data, a higher k might be beneficial. For large datasets, a smaller k might suffice.

Beyond the Basics

While standard k fold cross validation is widely used, variations exist for specific situations. This includes stratified k fold for imbalanced datasets and time series cross-validation for sequential data. The correct technique depends on your data characteristics and project goals. These advanced methods offer robust evaluation strategies for complex data scenarios. For further information on effective machine learning practices, explore machine learning infrastructure provided by DATA-NIZANT.

Evolution of K Fold Cross Validation: From Theory to Standard

K fold cross validation is a cornerstone of modern machine learning. But its path from theoretical idea to practical application is a compelling story of how increased computing power has unlocked advanced statistical methods. This journey underscores the essential role k fold cross validation plays in today’s machine learning landscape.

Early Statistical Validation Methods

Before the widespread adoption of k fold cross validation, simpler techniques like the holdout method were the norm. This method involved splitting the data into training and testing sets just once. The problem? This approach often led to high variance. The performance estimate depended heavily on the specific way the data was divided. This made it difficult to accurately gauge a model’s true performance.

The Rise of K Fold Cross Validation

The story of k-fold cross-validation is interwoven with the development of machine learning and statistical analysis. Although the fundamental concept of cross-validation has been around for a while, the practical use of the k-fold method took off in the 1990s. The rise of more powerful computers made the computationally demanding process of training and evaluating models on multiple data subsets feasible. Want to delve deeper? Learn more about k-fold cross-validation. Understanding the history provides valuable context for current best practices. For a broader perspective, explore this discussion on the evolution of predictive analytics.

Addressing Challenges in Model Reliability

K fold cross validation tackled the shortcomings of prior methods by providing a more robust way to estimate performance. How? By splitting the data into k folds and repeatedly using each fold as the validation set. This process minimizes the impact of any single data split. The result? A lower variance estimate of model performance, leading to a more dependable evaluation than the holdout method.

Refinement and Adoption by Leading Organizations

As k fold cross validation gained popularity, researchers and leading organizations continued to refine the technique. They developed adaptations to address specific data challenges, such as imbalanced datasets and time-series data. This led to the creation of specialized versions like stratified k fold and time series cross-validation, expanding its usefulness. These advancements cemented k fold cross validation as an indispensable tool in machine learning, boosting model reliability and predictive accuracy in various applications.

Hands-On Implementation Across Top ML Frameworks

Let’s dive into the practical application of k fold cross validation, moving beyond the theory. This hands-on exploration will show how this powerful technique is implemented in real-world machine learning projects. We’ll examine examples using popular frameworks like Scikit-learn, TensorFlow, and PyTorch, highlighting the strengths and differences of each.

K Fold Cross Validation With Scikit-Learn

Scikit-learn, a widely-used Python library, offers a streamlined approach to k fold cross validation. The KFold class simplifies data splitting and integrates seamlessly with various machine learning models.

The following code demonstrates a 5-fold cross validation example:

from sklearn.model_selection import KFold
import numpy as np

data = np.array([1, 2, 3, 4, 5, 6, 7, 8, 9, 10])
kfold = KFold(n_splits=5, shuffle=True, random_state=42)

for train_index, test_index in kfold.split(data):
X_train, X_test = data[train_index], data[test_index]
# Train your model on X_train and evaluate on X_test

This code initializes KFold with 5 splits, shuffles the data, and sets a random state for reproducibility. The loop then iterates through each fold, providing the indices for training and testing data.

Implementing K Fold Cross Validation in TensorFlow and PyTorch

While Scikit-learn emphasizes simplicity, TensorFlow and PyTorch require a more hands-on approach. This offers greater flexibility and control over the process. You manage the data splitting and iteration using the frameworks’ data loading and training tools. This means dividing your dataset into k folds and iteratively training and evaluating your model. For further exploration of ML infrastructure and deployment, you might find this article helpful: How to master Machine Learning Infrastructure.

Framework-Specific Optimizations

Each framework provides unique advantages. Scikit-learn shines in its ease of use. TensorFlow and PyTorch offer more granular control, enabling custom implementations and optimizations. For instance, TensorFlow’s tf.data API can optimize data loading and preprocessing within the cross-validation loop. PyTorch’s DataLoader provides similar functionality. These optimizations can be essential for reducing training time, particularly with large datasets.

To illustrate the differences further, let’s look at a comparison table:

To better understand the various implementation nuances, the following table compares K Fold Cross Validation across different frameworks:

K Fold Cross Validation Implementation Across Frameworks

Framework	Implementation Method	Key Functions/Methods	Special Features	Complexity
Scikit-learn	Built-in KFold class	KFold.split(), cross_val_score()	Simple, easy to use	Low
TensorFlow	Manual implementation with tf.data	tf.data.Dataset, custom loops	Flexible, optimized data handling	Medium
PyTorch	Manual implementation with DataLoader	torch.utils.data.DataLoader, custom loops	Flexible, optimized data handling	Medium

This table summarizes the key differences in implementing K Fold Cross Validation across the discussed frameworks, showcasing the trade-offs between simplicity and flexibility.

Handling Challenging Scenarios

K fold cross validation can be adapted to handle various data challenges. Stratified k fold maintains balanced class distributions across folds, crucial for imbalanced datasets. Time series cross validation respects the temporal order of data, essential when working with sequential data. These specialized methods are crucial for reliable results in complex scenarios.

Practical Considerations and Benchmarks

When using k fold cross validation, it’s important to consider the computational cost. Higher values of k provide more robust estimates but require more processing time. Performance benchmarks can help evaluate the balance between accuracy and computational resources. Understanding these trade-offs and the framework’s unique features allows you to select the optimal implementation for your specific task.

Finding Your Perfect K Value: Beyond the Defaults

Picking the right k value in k-fold cross-validation is a big deal for getting the best possible model performance. There’s no magic number; the ideal k depends on your data and what you’re trying to achieve. Values like 5 or 10 are common starting points, but really understanding how k works is essential for solid model evaluation.

The Impact of K on Statistical Validity and Computational Resources

Different k values influence both how reliable your statistical results are and how much computing power you need. A small k, such as 2, is computationally fast but can produce high variance in your performance estimates. This happens because each fold is a bigger chunk of your data, so any quirks within a single fold can skew the overall results. A larger k gives you more stable estimates by averaging across many folds but takes more time to compute.

Industry Practices and Evidence-Based Recommendations

Many machine learning professionals choose their k value based on the dataset itself, rather than sticking to standard defaults. For smaller datasets, a larger k is better to get the most out of limited data and make the performance estimates more stable. With massive datasets, a smaller k can be statistically sound while saving you valuable computing time. For instance, a k of 10 might be suitable for a dataset of 1000 samples. But for a dataset of only 200 samples, a larger k of 20 might be a smarter choice. You might be interested in: How to master Feature Selection Techniques.

K Selection’s Impact on Model Types and Validation Metrics

Your choice of k can also affect different model types and validation metrics differently. Models that tend to overfit, for example, might do better with a higher k for a more robust evaluation. Certain validation metrics are also more sensitive to variations between folds. Figuring out these relationships takes some experimentation and a data-focused approach.

Practical Frameworks for Choosing Your K

Here’s a simple guide to help you find the right k:

• Small Dataset (under 500 samples): Try a larger k (10-20) or even leave-one-out cross-validation, where k is the same as your sample size. This makes the most of every data point.
• Medium Dataset (500-1000 samples): k=10 often strikes a good balance.
• Large Dataset (over 1000 samples): Smaller k values (5-7) are often enough, saving you computation time.

Beyond Standard K Values: Leave-One-Out Cross-Validation

Leave-one-out cross-validation (LOOCV) is an extreme where k equals the number of data points. While computationally expensive, LOOCV can be useful with very small datasets, ensuring every single data point contributes to training and validation. However, it might be less reliable for models that easily overfit.

To understand how different k values affect model evaluation, consider the following table:

Impact of Different K Values on Model Evaluation

Statistical comparison of how different k values affect evaluation metrics across various dataset sizes.

K Value	Small Dataset Impact	Medium Dataset Impact	Large Dataset Impact	Computational Cost	Recommended Use Cases
2	High Variance	Moderate Variance	Low Variance	Low	Very large datasets, quick assessments
5	Moderate Variance	Low Variance	Low Variance	Moderate	Medium to large datasets
10	Low Variance	Low Variance	Low Variance	High	Small to medium datasets, standard choice
LOOCV	Very Low Variance	High Computational Cost	Extremely High Computational Cost	Extremely High	Very small datasets

As shown in the table, selecting the appropriate k-value involves balancing variance and computational cost. For small datasets, higher k values (like 10 or even LOOCV) offer lower variance but increase computational cost. For larger datasets, a smaller k like 5 or 7 usually provides a reasonable balance.

By thinking about these points and testing out different k values, you can fine-tune your k for your specific needs, leading to more dependable model evaluation and, ultimately, better performance.

Advanced K Fold Techniques for Specialized Challenges

Standard k fold cross validation is a powerful tool for evaluating machine learning models. However, it’s not a universal solution. Real-world datasets often present unique hurdles that demand more specialized k fold cross validation techniques. This involves adapting the standard method to handle complexities like imbalanced classes, time-based dependencies, and clustered observations. Let’s delve into some advanced techniques designed to tackle these specific challenges.

Stratified K Fold for Imbalanced Datasets

Consider building a fraud detection model. Fraudulent transactions are infrequent compared to legitimate ones, resulting in an imbalanced dataset. Standard k fold cross validation might inadvertently place a majority of the fraud cases into a single fold. This can skew the evaluation and lead to unreliable results. Stratified k fold resolves this by guaranteeing each fold maintains the same class proportions as the original dataset. This method offers a more accurate performance assessment, especially for the minority class, often the primary focus in imbalanced scenarios.

Time Series Cross Validation for Sequential Data

When working with time series data, such as stock prices or weather patterns, the chronological order is paramount. Standard k fold cross validation, which shuffles the data randomly, disrupts this vital temporal relationship. Time series cross validation takes this into account by constructing folds that respect the data’s inherent sequence. Each fold represents a contiguous time period. For instance, the initial fold might contain the oldest data, the second fold the next oldest, and so on. This ensures your model trains on past data and validates on future data, mirroring real-world predictive scenarios.

Group K Fold for Clustered Observations

Certain datasets contain clustered observations, where data points within a cluster exhibit greater similarity to each other than to those in other clusters. Examples include patients within hospitals, students within schools, or customers within specific geographic regions. Applying standard k fold in these cases could lead to data leakage. This occurs when data from the same cluster appears in both the training and validation sets, potentially inflating performance metrics. Group k fold prevents this by ensuring all data points from a single cluster are assigned to the same fold. This strategy accounts for correlations within clusters, yielding a more realistic evaluation of model generalization to unseen clusters. Learn more about practical applications in our article about How to master MLOps Best Practices.

Choosing the Right Technique

Choosing the correct k fold technique hinges on the characteristics of your data and the objectives of your analysis. Stratified k fold is essential for imbalanced datasets. Time series cross validation is the preferred method for sequential data. When dealing with clustered observations, group k fold becomes crucial. By understanding these advanced techniques, you can fine-tune your validation strategy, leading to more robust and dependable model evaluations.

Technique	Challenge Addressed	Key Feature
Stratified K Fold	Imbalanced Datasets	Preserves class proportions across folds
Time Series Cross Validation	Sequential Data	Respects temporal data order
Group K Fold	Clustered Observations	Keeps clustered data within the same fold

This table provides a concise overview of how each technique addresses a particular data challenge. It highlights the defining characteristic of each method, offering a clear roadmap for selecting the most appropriate approach. This is essential for developing accurate and robust models across diverse applications.

Avoiding the Hidden Pitfalls of Cross Validation

K-fold cross validation is a powerful technique for evaluating machine learning models. However, even seasoned data scientists can encounter subtle mistakes that diminish its effectiveness. These pitfalls can result in overly optimistic performance assessments and disappointing real-world outcomes. This section explores common errors and how to avoid them, helping ensure your models are truly ready for deployment.

Data Leakage: A Silent Saboteur

One of the most insidious pitfalls is data leakage, where information from the validation set unintentionally influences the training process. This can occur during preprocessing steps like feature scaling or missing value imputation. For example, if you scale your entire dataset before applying k-fold cross-validation, information about the distribution of the validation set leaks into the training data. This artificially inflates performance during cross-validation, a boost that won’t materialize in real-world applications. The solution? Perform preprocessing steps within each fold of the cross-validation loop. This guarantees each fold’s independence.

Misinterpreting Variance Across Folds

Significant performance fluctuations between folds signal a problem. This high inter-fold variance indicates the model’s sensitivity to the specific data within each fold. Possible causes include a limited dataset, excessive model complexity, or an unsuitable choice of k. Investigating the source of this variance is paramount. Adjusting k, opting for a simpler model, or collecting more data might be necessary for a stable evaluation.

Overlooking Data Characteristics

Standard k-fold cross-validation operates under the assumption that data points are independent and identically distributed (IID). This assumption doesn’t hold true for certain data types. Applying standard k-fold cross-validation to time series data, for instance, can lead to inaccurate performance estimates due to temporal dependencies. Similarly, if your data exhibits clustered observations (e.g., patients grouped within hospitals), standard k-fold might underestimate the true generalization error. In these cases, specialized techniques like time series cross-validation or group k-fold are crucial for obtaining reliable results.

When K-Fold Isn’t the Answer

While k-fold cross-validation offers versatility, it’s not always the optimal choice. For massive datasets, the computational cost can be prohibitive. In these situations, techniques like hold-out validation with a sufficiently large test set might be more practical. Furthermore, with highly imbalanced datasets, even stratified k-fold can struggle. Techniques like bootstrap sampling can provide a more robust evaluation under such circumstances.

Practical Safeguards for Trustworthy Evaluation

Here are some best practices to enhance the reliability of your k-fold cross-validation results:

• Preprocess within each fold: Isolate each fold by performing scaling, imputation, or encoding separately within the cross-validation loop, preventing data leakage.
• Evaluate inter-fold variance: Examine significant performance differences between folds to pinpoint potential problems with your model or data.
• Consider data characteristics: Employ specialized cross-validation techniques when dealing with time series data, clustered observations, or other non-IID data structures.
• Choose appropriate k: Strike a balance between computational expense and variance reduction when selecting k. Common values like 5 or 10 often serve as good starting points, but experimentation is key to finding the optimal value for your specific data.

By understanding and addressing these common pitfalls, you can ensure your k-fold cross-validation provides an accurate representation of your model’s performance. This leads to better model selection, more effective hyperparameter tuning, and ultimately, more successful machine learning projects.